Question: 找到丢失的数字
现在你手上有n-1个数字, 这些数字的范围是[1, n]且这n-1个数字中没有重复的数字.
由上述条件可知: 你手上的数字丢失了一个.
请编写一段高效的找到该确实数字的代码.
考察需求
首先你应该要对面试官问的这道题的需求, 在这里就是这个数字列表是有序的还是无序的? 那么你问了面试官之后呢, 面试就告诉你了, 这就是一个良好的开始.
考察思路:
- 首先需要问清楚题目意思
- 这个数字列表是有序的还是无序的?
- 考虑各种方法的时间复杂度, 空间复杂度
- 算法的思路
- 第一步应该怎么做
- 第二步应该怎么做
- 程序实现
- 能不能写出一些测试用例, test_case, 用我们写好的程序跑过去?
实现思路(5种)
第1种: 先排序, 再用二分法
使用二分法
- 这就涉及到我们的List是有序的还是无序的?
先排序, 再用二分法
- 这就涉及到各种排序算法的优劣性
- List.sort()或者sorted(List)
第2种: 先排序, 再用线性的查找方式
- 也就是for循环呗, 每次看这个 i 等不等于上一个 i+1
- 不等于的话就把当前的 i 打印出来
第3种: 先求和(速度非常快)
首先我们是缺少了一个数字对不对?
- 我们可以把这些数字加起来, 求和, 记为 sum_now
然后如果我们 1~n 的数字都存在的话, 原本的1到n的累加和我们是不是已经知道了
- 也就是 (1+n) * n / 2
- (首相+末项) × 项数 ÷ 2
- 记为 sum_all
那么 sum_all - sum_now 就能得出我们缺失的那个数字
第4种: 计数排序
可以理解为现在我们有 n 个抽屉, 编号 1~n 号
然后我们遇到一个数字, 就把这个数字放到抽屉里面去
- 这个是5我们放到第5个抽屉
- 这个是8我们放到第8个抽屉
当所有数过完一遍后, 我们看那个抽屉是空的, 我们是不是就知道哪个数缺失了
第5种: XOR 异或
(速度是最快的, 异或操作比加减乘除都要快, 因为计算机是要做加减乘除的时候要先转换成二进制再进行计算, 所以直接在二进制层面上的异或操作是最快的)
0^1 = 1
0^0 = 0
1^0 = 1
1^1 = 0
A^A = 0
A^0 = A
a⊕b = (¬a ∧ b) ∨ (a ∧¬b)
如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0。
支持交换律
- A^B^C = C^B^A = …
计算机中数的运算转换成二进制进行的, 比如说我们的 3 转换成二进制就是 0011, 8 转换成二进制就是 1000
做法:
我们先拿 1异或2一直异或到n
- 1^2^3^4^…^n
再和我们的乱序List的异或作比较
- a0 ^ a1 ^ a2 ^ …^ 0 ^ … ^ an-2
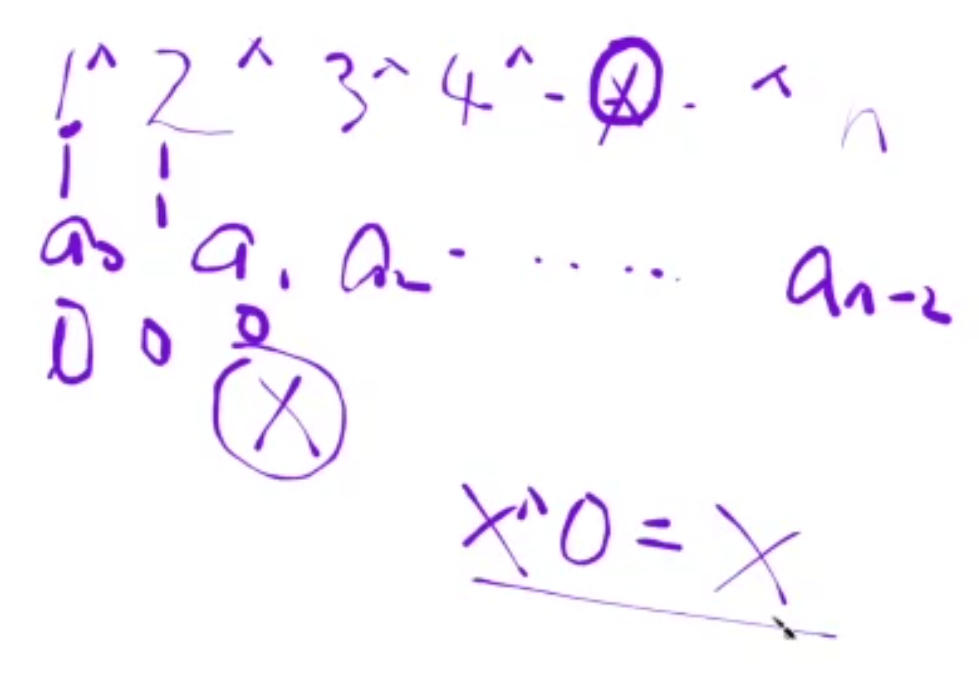
1,2,3,…异或下面的都得到0, 只剩 x 异或下面的 0(因为那个数已经缺失了, 所以是0), 得到 x
那么这个 x 就是我们丢失的数字
tips:
98765 * 32
等同于
98765 * 2^5
等同于在二进制上左移5位-> 位操作
1 | 98765<<5 |
是一样的

