ArrayList Excecises

收集python列表相关的题目

Ex: 计算素数(质数)

设计一个计算素数的函数

prime(n), 素数的个数小于等于n,
举个栗子: prime(17)=7, 因为前7个素数为2, 3, 5, 7, 11, 13, 17

''' 
计算素数 (1)
	时间复杂度: O(n^2), 对于n个数字中的每一个都要遍历1到根号n
	空间复杂度: O(1) 
''' 
import math 
def prime(number):
    n = 0
    for i in range(2, int(math.sqrt(number)) + 1): 
        if number % i == 0: 
            n += 1
        if n == 0:
            return True
        return False

prime_nums = []
    for i in range(20):
        if prime(i):
            prime_nums.append(i) 

print(len(prime_nums))
print(prime_nums)

'''
计算素数 (2): 用空间换时间
    时间复杂度: O(n), 只需要遍历一遍数组
    空间复杂度: O(2n)
    
	tips: if判断是非常快的, 比根号n快多了
'''

def count_prime(n): 
    is_prime = [True] * (n + 1) # 首先假设1到n中的所有数都是质数, 为True 
    i = 2
    while (i * i <= n): # 遍历, 当 i**2 < n 的时候, 
        if (is_prime[i]): # 先判断 i 是否为素数 
            j = i # 是的话, 把i赋值给j 
            while (j * i <= n): # 当 j * i <= n 时, 
                is_prime[i * j] = False # 把 i 的倍数的数设置为False, 因为已经有 i 这个因数了 
                j += 1 # j自增, 把i的所有倍数都设为非质数 
        i += 1 # i自增
    # 统计素数个数 
    count = 0 
    for i in range(2, n+1): 
        if (is_prime[i]): 
            count += 1 
            print(i, end = " ") 
    return count

# 计算从从1到100范围内的素数个数 
count_prime(100)

Ex: 验证哥德巴赫猜想

1742年, 哥德巴赫提出了著名的哥德巴赫猜想. 即: 任一大于2的偶数都可以写成两个质数之和. 比如说16=3+13.

试着编码出程序: 只包含n作为参数, 并且给出n为两个质数之和的表达式.

哥德巴赫猜想至今没有被证明, 但是目前已知其在n<10^14的时候都是成立的.

'''
验证哥德巴赫猜想
'''
import math
import time

# 判断素数
def check(num):
    for i in range(2, int(math.sqrt(num)+1)):
        if num % i == 0:    
            return False  
        return True


start = time.time() 
flag = 0 # 初始化标志位 
for i in range(2, 50001): 
    test_num = i*2 
    for j in range(2, test_num-2):
        if check(j) and check(test_num-j):
            # print(test_num, "满足哥德巴赫猜想")
            flag = 1
            break 
		else:
            flag = 0 
            if j == test_num-2: 
                print(test_num, "不满足哥德巴赫猜想")
if flag == 1: 
	print("在数字2~100000之间，哥德巴赫猜想成立")


end = time.time() 
res = end - start
print(res)

Ex: 扫雷游戏

我们来写一个小程序：

程序接收三个参数，M，N和p，然后生成一个M * N的矩阵，然后每一个cell(小格子)有p的概率是地雷。生成矩阵后，再计算出每一个cell周围地雷的数量。

代码实现

import random


# 定义生成棋盘函数
def sweeper(m, n, p):
    # tips: 生成m+2&n+2的初始棋盘来避免边界判断, -1代表雷
    board = [[None] * (n + 2) for i in range(m + 2)]
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            r = random.random()
            board[i][j] = -1 if r < p else 0

    # 绘制棋盘
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            print("*", end=" ") if board[i][j] == -1 else print(".", end=" ")
        print()

    # 计算每个格子的值
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if (board[i][j] != -1):
                # 计算四周的地雷数量
                for ii in range(i - 1, i + 2):
                    for jj in range(j - 1, j + 2):
                        if (board[ii][jj] == -1):
                            board[i][j] += 1

    print()
    # 打印结果
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            print("*", end=" ") if board[i][j] == -1 else print(board[i][j], end=" ")
        print()


# 生成10x10, 概率p=0.2的扫雷棋盘
sweeper(10, 10, 0.2)

展示效果:

>. . . . . . . . . . 
>. . . . * * . . . * 
>. . . . . * * * * . 
>. . . . . . * . * . 
>. . . . . . . . . . 
>. . . . . . . . . * 
>. * . . * . * . . . 
>. . . . * . . . . . 
>. * . * . * . . . * 
>* . . . . * . * . . 
>
>0 0 0 1 2 2 1 0 1 1 
>0 0 0 1 * * 4 3 3 * 
>0 0 0 1 3 * * * * 3 
>0 0 0 0 1 3 * 5 * 2 
>0 0 0 0 0 1 1 2 2 2 
>1 1 1 1 1 2 1 1 1 * 
>1 * 1 2 * 3 * 1 1 1 
>2 2 3 3 * 4 2 1 1 1 
>2 * 2 * 4 * 3 1 2 * 
>* 2 2 1 3 * 3 * 2 1 
>

tips: 第7行代码是精髓, 有很多时候可以通过简单的方法来避免繁琐的边界判断过程

Ex: 矩阵0变换

给一个m×n的矩阵，如果有一个元素为0，则把该元素对应的行与列所有元素全部变成0。

matrix = [  [ 1, 1, 1, 1, 1, 0, 1, 1, 1, 1 ],
            [ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 ],
            [ 1, 1, 0, 1, 1, 1, 1, 1, 1, 1 ],
            [ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 ],
            [ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 ] ]

也就是变成这样 ↓

matrix =[ [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
          [1, 1, 0, 1, 1, 0, 1, 1, 1, 1],
          [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
          [1, 1, 0, 1, 1, 0, 1, 1, 1, 1],
          [1, 1, 0, 1, 1, 0, 1, 1, 1, 1] ]

思路1: 先想第一种, 我再去创建一个 m×n 的数组(matrix), 然后这个数组里面专门存0的位置, 就是把0的位置设置为True;

这种方法需要用到额外mxn的空间→空间复杂度O(m×n)

思路2: 用set, 一个放行, 一个放列;

当然可以, 不过这个题先用列表来做

思路3: 我们是否需要维持(maintain)一个 m×n 的数组? 是可以不需要的; 只需要两个一维数组就够了, 一个maintain哪些列有0, 另一个maintain哪些行有0;

这种方法的空间复杂度为O(m+n) →space complexity

def zero(matrix):
    m = [None] * len(matrix)  # 行
    n = [None] * len(matrix[0])  # 列
    for i in range(len(matrix)):  # 遍历行
        for j in range(len(matrix[0])):  # 遍历列
            if (matrix[i][j] == 0):  # 如果出现了0了
                m[i] = 1  # 就把这一行设为1
                n[j] = 1  # 就把这一列设为1
	
    # 通过m和n两个一位数组, 修改原有矩阵(matrix)
    for i in range(len(matrix)):
        for j in range(len(matrix[0])):
            if (m[i] == 1 or n[j] == 1):
                matrix[i][j] = 0

matrix = [  [ 1, 1, 1, 1, 1, 0, 1, 1, 1, 1 ],
            [ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 ],
            [ 1, 1, 0, 1, 1, 1, 1, 1, 1, 1 ],
            [ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 ],
            [ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 ] ]

1
2
3

# 原有matrix
for x in matrix:
    print(x, sep=" ")

># 输出
>[1, 1, 1, 1, 1, 0, 1, 1, 1, 1]
>[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
>[1, 1, 0, 1, 1, 1, 1, 1, 1, 1]
>[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
>[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
>

↓↓↓

# 修改后matrix
zero(matrix)
for x in matrix:
    print(x, sep=" ")

># 输出
>[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
>[1, 1, 0, 1, 1, 0, 1, 1, 1, 1]
>[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
>[1, 1, 0, 1, 1, 0, 1, 1, 1, 1]
>[1, 1, 0, 1, 1, 0, 1, 1, 1, 1]
>

Ex: 九宫图

def magic_square(n):
    magic = [[0] * (n) for i in range(n)]
    row = n - 1
    col = n//2
    magic[row][col] = 1
    
    for i in range(2, n * n + 1):
        try_row = (row + 1) % n
        try_col = (col + 1) % n

        if (magic[try_row][try_col] == 0):
            row = try_row
            col = try_col
        else:
            # row往上移1行, 有可能会产生负数, 所以+n
            row = (row - 1 + n) % n  
        
        magic[row][col] = i
    
    for x in magic:
        print(x, sep=" ")

1	magic_square(3)

># 输出
>[4, 9, 2]
>[3, 5, 7]
>[8, 1, 6]
>

1	magic_square(5)

># 输出
>[11, 18, 25, 2, 9]
>[10, 12, 19, 21, 3]
>[4, 6, 13, 20, 22]
>[23, 5, 7, 14, 16]
>[17, 24, 1, 8, 15]
>

Ex: 数独

给一个填好的数独，验证是否正确

matrix = [
    [5,3,4,6,7,8,9,1,2],
    [6,7,2,1,9,5,3,4,8],
    [1,9,8,3,4,2,5,6,7],
    [8,5,9,7,6,1,4,2,3],
    [4,2,6,8,5,3,7,9,1],
    [7,1,3,9,2,4,8,5,6],
    [9,6,1,5,3,7,2,8,4],
    [2,8,7,4,1,9,6,3,5],
    [3,4,5,2,8,6,1,7,9]
]

def sudoku(matrix):
    n = len(matrix)
    result_row = result_col = result_blk = 0

    for i in range(n):
        result_row = result_col = result_blk = 0
        for j in range(n):
            ## check row
            tmp = matrix[i][j]
            if ((result_row & (1 << (tmp-1))) == 0):
                result_row = result_row | (1<<(tmp-1))
            else:
                print("row: ", i, j)
                return False

            ## check column
            tmp = matrix[j][i]
            if ((result_col & (1 << (tmp-1))) == 0):
                result_col = result_col | (1<<(tmp-1))
            else:
                print("col: ", j, i)
                return False

            ## check block
            idx_row = (i//3) * 3 + j//3
            idx_col = (i%3)  * 3 + j%3
            tmp = matrix[idx_row][idx_col]
            if ((result_blk & (1 << (tmp-1))) == 0):
                result_blk = result_blk | (1<<(tmp-1))
            else:
                print("block: ", idx_row, idx_col)
                return False
    return True

1	sudoku(matrix)

1
2

> True
>

Ex: 旋转数组

给一个n×n的数组，顺时针旋转90度。

'''
空间复杂度: O(n^2)
'''
def rotate(matrix):
    n = len(matrix)
    result = [[0] * (n) for i in range(n)]
    
    for i in range(n):
        for j in range(n):
            result[j][n-1-i] = matrix[i][j]
    
    for x in result:
        print(x, sep=" ")

1 2	matrix = [[i*5+j for j in range(5)] for i in range(5)] matrix

> [[0, 1, 2, 3, 4],
>  [5, 6, 7, 8, 9],
>  [10, 11, 12, 13, 14],
>  [15, 16, 17, 18, 19],
>  [20, 21, 22, 23, 24]]
>

1	rotate(matrix)

>[20, 15, 10, 5, 0]
>[21, 16, 11, 6, 1]
>[22, 17, 12, 7, 2]
>[23, 18, 13, 8, 3]
>[24, 19, 14, 9, 4]
>

# in-place: 不使用额外空间, 在原有数组上进行修改
def rotate_in_place(matrix):
    n = len(matrix)
    for layer in range(n//2):
        first = layer
        last = n - 1 - layer
        for i in range(first, last):
            offset = i - first
            top = matrix[first][i]  # save top
            
            ## left->top
            matrix[first][i] = matrix[last-offset][first]
            
            ##bottom -> left
            matrix[last-offset][first] = matrix[last][last - offset];

            # right -> bottom
            matrix[last][last - offset] = matrix[i][last];

            # top -> right
            matrix[i][last] = top;  # right <- saved top            
            
    for x in matrix:
        print(x, sep=" ")

1 2	matrix = [[i*5+j for j in range(5)] for i in range(5)] rotate(matrix)

> [20, 15, 10, 5, 0]
> [21, 16, 11, 6, 1]
> [22, 17, 12, 7, 2]
> [23, 18, 13, 8, 3]
> [24, 19, 14, 9, 4]
>

Ex: 反转字符串

1 2	def reverse(s): return s[::-1]

1
2
3

s = "hello"
r = reverse(s) # O(n)
r

‘olleh’

def reverse2(s):
    l = list(s)
    for i in range(len(l)//2):
        l[i], l[len(s)-1-i] = l[len(s)-1-i], l[i]
    return ''.join(l)

1
2
3

s = "hello"
r = reverse2(s)
r

‘olleh’

Ex: 最大连续子串

给定一个数组，数组里有一个数组有且只有一个最大数，判断这个最大数是否是其他数的两倍或更大。如果存在这个数，则返回其index，否则返回-1。

Example:
Input: [1,1,0,1,1,1]
Output: 3

def find_consecutive_ones(nums):
    """
    local: 当前1出现的次数
    maximum: 历史上1出现的最大次数
    """
    local = maximum = 0
    for i in nums:
        local = local + 1 if i == 1 else 0
        maximum = max(maximum, local)
    return maximum

1
2
3

nums = [1,1,0,1,1,1,1,0,0,0,0,0,1,1,1,0,0,1]
result = find_consecutive_ones(nums)
result

Ex: 最大数

给定一个数组，数组里有一个数组有且只有一个最大数，判断这个最大数是否是其他数的两倍或更大。如果存在这个数，则返回其index，否则返回-1。

简化思路: 不需要将最大数与每个数都比较, 只要和第二大的数比较就行

# O(n) time
# O(1) space
def largest_twice(nums):
    maximum = second = idx = 0
    for i in range(len(nums)):
        if (maximum < nums[i]):
            second = maximum
            maximum = nums[i]
            idx = i
        elif second < nums[i]:
            second = nums[i]
    return idx if (maximum >= second * 2) else -1

1
2
3

nums = [1, 2,3,8,3,2,1]
result = largest_twice(nums)
result

Ex: Find All Numbers Disappeared in an Array

Given an array of integers where 1 ≤ a[i] ≤ n (n = size of array), some elements appear twice and others appear once.

Find all the elements of [1, n] inclusive that do not appear in this array.

Could you do it without extra space and in O(n) runtime?
You may assume the returned list does not count as extra space.

题目: 30s给爷找出列表中没了的数字
给定一个整数数组，其中1≤a[i]≤n(n=数组大小)，有些元素出现两次，而另一些元素出现一次。

查找[1，n]中没有出现在此数组中的所有元素(包括[1，n])。

你可以在没有额外空间的情况下(抽屉原理否决)在O(N)运行时间内完成吗？
你可以假定返回的列表不算额外空间。

Example:
Input: [4,3,2,7,8,2,3,1]
Output: [5,6]

# O(n^2)
def findDisappearedNumbers1(nums):
    result = []
    for i in range(1, len(nums) + 1):
        if (i not in nums):
            result.append(i)
    return result

1 2	nums = [4,3,2,7,8,2,3,1] print(findDisappearedNumbers1(nums))

[5, 6]

def findDisappearedNumbersTest1(nums):
    start = time.time()
    r = findDisappearedNumbers1(nums)
    t = time.time() - start
    return r, len(nums), t

import time
import matplotlib.pyplot as plt
import random
import math
%matplotlib inline  

def random_list(l):
    return [[i + 1 for i in range(l * n)] for n in range(1, 20)]

random_lists = random_list(100)
rst = [findDisappearedNumbersTest1(l) for l in random_lists]
len(rst)
rst

[([], 100, 0.0),
([], 200, 0.0),
([], 300, 0.0009765625),
([], 400, 0.0009758472442626953),
([], 500, 0.0009756088256835938),
([], 600, 0.0019519329071044922),
([], 700, 0.0039052963256835938),
([], 800, 0.004901885986328125),
([], 900, 0.004884481430053711),
([], 1000, 0.007781982421875),
([], 1100, 0.006831169128417969),
([], 1200, 0.009760379791259766),
([], 1300, 0.009790897369384766),
([], 1400, 0.014636039733886719),
([], 1500, 0.014640092849731445),
([], 1600, 0.014611959457397461),
([], 1700, 0.017599105834960938),
([], 1800, 0.019518375396728516),
([], 1900, 0.02632427215576172)]

x = list(zip(*rst))[1]
y = list(zip(*rst))[2]

plt.plot(x, y)

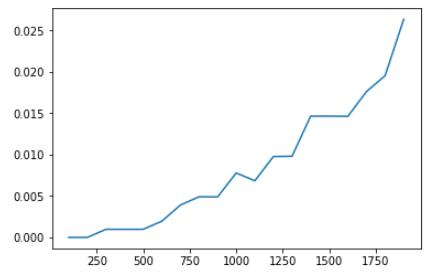
时间复杂度O(n^2)

# 思路: 把下标当成数组, 出现过的数字下标会被改变, 没有改变的是缺失的数
def findDisappearedNumbers2(nums):
    # For each number i in nums,
    # we mark the number that i points as negative.
    # Then we filter the list, get all the indexes
    # who points to a positive number
    for i in range(len(nums)):
        index = abs(nums[i]) - 1
        nums[index] = - abs(nums[index])

    return [i + 1 for i in range(len(nums)) if nums[i] > 0]

1 2	nums = [4,3,2,7,8,2,3,1] print(findDisappearedNumbers2(nums))

[5, 6]

# O(n)
def findDisappearedNumbersTest2(nums):
    start = time.time()
    r = findDisappearedNumbers2(nums)
    t = time.time() - start
    return r, len(nums), t

random_lists = random_list(100)
rst = [findDisappearedNumbersTest2(l) for l in random_lists]
len(rst)
rst

[([], 100, 0.0),
([], 200, 0.0),
([], 300, 0.0),
([], 400, 0.0),
([], 500, 0.0009999275207519531),
([], 600, 0.0010001659393310547),
([], 700, 0.0009999275207519531),
([], 800, 0.0),
([], 900, 0.01399993896484375),
([], 1000, 0.0),
([], 1100, 0.0010001659393310547),
([], 1200, 0.0009999275207519531),
([], 1300, 0.0),
([], 1400, 0.0009999275207519531),
([], 1500, 0.0010001659393310547),
([], 1600, 0.0009999275207519531),
([], 1700, 0.0009999275207519531),
([], 1800, 0.0019998550415039062),
([], 1900, 0.0010004043579101562)]

1
2
3

x = list(zip(*rst))[1]
y = list(zip(*rst))[2]
plt.plot(x, y)

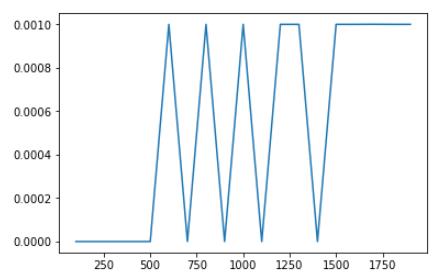
时间复杂度O(n)

Ex：Plus One

Given a non-negative integer represented as a non-empty array of digits, plus one to the integer.

You may assume the integer do not contain any leading zero, except the number 0 itself.

The digits are stored such that the most significant digit is at the head of the list.

翻译:
比如说有个digits = [1, 2, 3]
就需要得到: [1, 2, 4]

比如说有个digits = [9, 9, 9]
就需要得到: [1, 0, 0, 0]

def plusOne(digits):
    if len(digits)==0:
        return False
    addCarry=1
    for i in range(len(digits)-1,-1,-1):
        digits[i]+=addCarry
        if digits[i]==10:
            digits[i]=0
            if i==0:
                digits.insert(0,1)
        else:
            break
    return digits

digits = [1, 2, 3]
print(plusOne(digits))
digits = [9, 9, 9]
print(plusOne(digits))

[1, 2, 4]
[1, 0, 0, 0]